Series Xc Antenna Tuning

Earlier this year I was helping a friend install and tune a 40 meter vertical that he had purchased at a flea market. It was made from large aluminum tubes of constant diameter and was therefore a fixed length (height). It was mechanically sound but required rope guys and a post for support.

He had prepared 16 radials of about 10 meters length -- about ¼λ -- which we stapled to the ground. It was directly fed with coax, without a matching network. The match was poor. The antenna resonated about 300 kHz too low, well outside the band. I suspected that the radials were too long, but cutting them was not an option.

Not being allowed to cut the radials or the vertical, there were still a few options. I studied the antenna with an analyzer for a few minutes to characterize its impedance. At resonance (outside the band) the impedance was approximately 37 Ω (I don't recall the exact value). This is typical for a vertical with low ground loss. However, as the frequency increased the R value also increased, along with the inductive reactance X. R was close to 50 Ω between 7.0 and 7.1 MHz (again, I forget the exact values).

This was a blessing and a curse. A blessing because only a series capacitor was needed to cancel the inductive reactance to provide a good SWR curve across most of the band, but a curse because I didn't have suitable capacitors on hand, fixed or variable. To my surprise, my friend had a large supply of ancient mica transmitting capacitors. All I needed to do was find the right one.

Rather than guess, we did the simple math to calculate the capacitor value that would equal the measured inductive reactance near the centre of the spectrum that of interest: 7.1 MHz. The value came to 400 pf. 

The equation, which all hams ought to know, is Xc = 1/(2πfC). Look carefully at that equation if you are unfamiliar with it: the smaller the capacitance, the greater the reactance. Large values that have a very low reactance (at the design frequency) can be found in lightning arresters and bias-T circuits to block DC while passing RF.

I rooted through the box until I found a capacitor that was suitable for 1000 watts and close to the desired value. That was a beefy 330 pf mica capacitor. I connected it in series and measured an excellent SWR curve. We made the connection more permanent and left my friend to add a weatherproof enclosure later. The antenna continues to work well.

This approach to antenna matching is similar to that for gamma matches where you find the tap point on the element where R is close to 50 Ω and then use a series capacitor to cancel the inductive reactance, resulting in a 50 + j0 Ω match at the selected centre of the operating bandwidth. There are other potential applications. 

Consider the SWR curves for two antennas resonant (X = 0) at 3600 kHz, for CW and digital modes. The vertical has a "perfect" ground, or one simulated with an extensive radial field, and the inverted vee is 30 meters above EZNEC medium ground.

Now suppose that you want to also have a low SWR for SSB high in the band, say 3900 kHz. You have several choices, and you can probably think of more:

• Make it a fan dipole/vertical, with the parallel element tuned for higher in the band.
• Cut the antenna for 3900 kHz and have a switchable coil at the base or partway along the element (each half-element of the inverted vee).
• Switched L-network or similar to match the antenna at 3900 kHz.
• Switched series capacitor to improve SWR in the SSB segment, if the R value is suitable.

Note that both antennas are not a perfect 50 Ω match for CW, though the SWR is close enough in most cases, especially when an antenna tuner is used. The vertical is more broadband than the inverted vee (or dipole), which is typical. Although the omni-directional mode of my 80 meter yagi (driven element as a simple vertical) has a reasonably low SWR up to 3800 kHz, I included a switched L-network to lower it further for SSB to "future proof" it in case I purchase a broadband solid state amplifier.

Getting back to those two example antennas, SWR curves are inadequate to determine whether it is possible to insert a series component to match the antenna for the SSB segment of 80 meters. We need to calculate or, better, measure R and X across the operating range. For reliable measurements you should use a modern single-port antenna analyzer or VNA of known accuracy, especially for large deviations from the nominal 50 + j0 Ω impedance. I use RigExpert but there are other excellent products on the market.

For this exercise I'll stick with calculations by EZNEC. Although I mostly used the NEC5 engine for the models in this article, NEC2 is perfectly good for these simple antennas, and it comes free with EZNEC. Below is a plot of the R and X values for both antenna models.

One striking difference is that the inverted vee's X (reactance) changes more rapidly with frequency. That's the reason for its narrower SWR bandwidth. Also, notice the slow change in R for both antennas, which increases with frequency. Finally, there is an excellent linear frequency relationship of both R and X. However, that is only true for small percentage frequency ranges. Other antenna types will have different curves.

The relationship scales: the chart is for 80 meters but the same is true for my friend's 40 meter antenna. It should be clear why I was inspired by the antenna feed point's measured R and X.

We can cancel the inductive reactance with a series capacitor to shift the SWR curve higher in the band. Of course it isn't quite that simple. First, since R will remain the same, that will determine the minimum SWR in a 50 Ω system. On the chart you can see that the vertical is more promising than the inverted vee. Second, the quality of the capacitor is critical. It must have a high Q so that very little power is dissipated by the devices ESR (equivalent series resistance) or it will fail with high power. Good transmitting capacitors (see the earlier article reference) should have a Q of at least 1000 so that the ESR is low enough for high power. Solve for R in Q = X / R and then use that in P = I²R to calculate the power dissipation. Unlike coils, capacitors are small so their construction and surface area to conduct heat away can be critical if the loss is more than a few watts.

For the vertical it is easy to find the correct capacitor value by calculation or trial and error in EZNEC. To bring X to zero at 3900 kHz the capacitor value is 835 pf. There are no commercial capacitors with that value so it would have to be done with a combination of capacitors or a variable capacitor, with or without a parallel fixed capacitor. EZNEC also helpfully calculates the power dissipation if you provide the ESR. For a capacitor with a Q of 1000 the calculated loss is almost exactly 1 watt for a transmitter power of 1000 watts.

We are not so lucky with the inverted vee due to that high R of about 94 Ω at 3900 kHz. This is a case where a two-component L-network is preferred in order to transform both R and X to achieve a better SWR. The same is true for an inverted vee tuned to resonance at 3900 kHz and brought down to 3600 kHz with coils.

It should also be noted that since the inverted vee is a balanced antenna, a series capacitor in each leg is required to preserve balance. In this case the capacitance reactance in each leg must be less because they are in series. That is achieved with a higher value capacitor of 550 pf versus about 280 pf if a single capacitor is used. You can use one capacitor but should not because the antenna becomes unbalanced and common mode current is more likely and a CMC choke with a higher impedance is needed to avoid excess heating.

At this point I'll reveal that I have an underlying motive other than what I've discussed. On my list for new projects is my longstanding desire to make my 80 meter 3-element wire yagi a yagi on SSB. It is only a yagi in the CW segment at present. A 4-square on 80 meters works from 3.5 to 3.8 MHz (the 80 meter segment of interest to me) while a yagi is too narrow band, only covering 3500 to 3650 kHz. Shifting the antenna upward 150 kHz would achieve my objective.

I won't get it done this year, so there is time to consider alternatives. A series capacitor in all 5 elements is one of the options. The approach has several advantages:

• High efficiency: High Q capacitors are easier than high Q coils.
• Small size: A capacitor and relay will fit inside the existing PVC electrical boxes.
• Switching: SSB relay lines to the parasitic elements is already installed. The SSB selector line at present is only used to modify the L-network for the driven element in omni-directional mode.
  

Until now my plan was to place two coils in the parasitic element switch boxes. With the element tuned as a director for SSB, one coil would shift resonance downward to make it a reflector (as is currently done) and the second to move resonance downward from SSB to CW.

As a CW reflector there would be two series coils. That would further reduce the already low radiation resistance (due to the T-shaped parasitic wire elements) and incur loss in the coils. Getting coil Q high enough to avoid significant loss would require new enclosures to fit two of them in a manner that avoids stray coupling.

By using a series capacitor these difficulties can be largely circumvented. The new difficulty is finding enough of the needed low loss, high RF current capacitors of the required value. But first, let's determine the capacitor value and its performance using an EZNEC model.

For yagi operation from 3500 to about 3650 kHz the director is tuned to 3680 kHz and the reflector to 3450 kHz. By opening the shorting relay, the series coil shifts resonance downward by 230 kHz. For use between 3650 and 3800 kHz, the parasitic resonances shift 150 kHz upward to 3600 and 3830 kHz. 

The height of the driven element (tower + stinger) is difficult to adjust so an L-network tunes the antenna for yagi mode (all 4 directions) and for both CW and SSB omni-directional modes. In any case, feed point R is quite low for yagi mode and below 35 Ω in omni-directional mode.

My first question was how much the parasitic element's R would change when inserting the appropriate value of series capacitor at the feed point. For the required 150 kHz upward shift the capacitor value is 1400 pf. R increases from 21.4 Ω to 23.8 Ω, or about 10%. That's for perfect ground. When ground loss is added the percentage change is less since it is in series with the feed point. 

The percentage change is less when it is made a reflector by switching in the 2.1 μH coil. R is 23.9 Ω at 3450 kHz (CW) and 25.8 Ω at 3600 kHz (SSB).

That's promising since the impedance is roughly the same for parasitic elements tuned to either CW or SSB by the series capacitor. If the same can be done for the driven element, a fixed L-network can be used for all yagi and omni-directional modes. That can now be tested in the model.

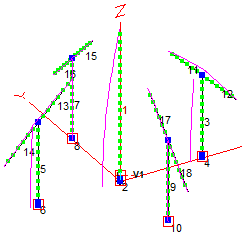
I pulled out my old EZNEC model of the completed 80 meter yagi. There were several design iterations before construction began, and this is the one that was built. In the EZNEC view, the antenna direction is to the right.

I used NEC2 since NEC5 introduced small differences that I didn't want to spend time on even though the result is certainly more accurate due to the acute angle on one side of the T-shaped parasitic elements. Continuing with NEC2 does not substantially affect the present study. I'll switch to NEC5 when I am ready to proceed with the project.

The L-network for the yagi modes was refined to make the SWR curve as good as it can be. When I built the antenna, I used the model as a guide but built the matching networks based on measurements. The two were pretty close. 

SWR curves for CW were calculated and then 1400 pf series capacitors were inserted at the base of the 3 active elements (the inactive elements are floated) to, hopefully, shift the array to the SSB contesting part of the band, which is roughly 3650 to 3800 kHz. 

The driven element reactance is not the same as the reflector and director so I manually adjusted the capacitor until the SWR curves were roughly alike. The capacitor for the driven element is 3000 pf (less inductive reactance to cancel).

The curves are almost identical. I expected them to be close but not this close. The impedance change for the 150 kHz upward shift is quite modest so the same L-network at the driven element feed point works very well for both CW and SSB. 

However, we have not yet demonstrated that the yagi's performance is similar. I did that next.

To my eyes they're identical. In fact, the SSB performance is marginally better. Performance lags in the top 50 kHz for both CW and SSB, which was already known from the original design. Yagis, which are high Q antennas, are challenged on 80 meters where the percentage span of the operating range is high, in this case over 4%. That's equivalent to 300 kHz on 40 meters and 600 kHz on 20 meters.

The low gain is due to near field and far field ground loss, typical of verticals. It's worse with yagis since the radiation resistance is low. 4-squares perform better. I have plans to improve antenna performance, which I hope to implement next year. 

Series capacitors to support SSB appear to be a good technique to apply to the current and future version of the 80 meter yagi. It's simple, efficient (with the right capacitor) and predictable. All I have to do now is scrounge those 5 capacitors.